如何计算最佳投注本金?

- 阅读:体育博彩玩家最常犯哪些错误?
预期价值这一概念最早由法国数学家斯卡尔和费马为了解决点数分配问题于17世纪提出。通过它,我们可以知道投注的平均预期利润。然而,这个概念并没有办法帮助博彩玩家判断出投注应该使用多少风险本金,而这正是预期效用发挥作用的地方。
预期价值和预期效用解析
投注预期价值(EV)的计算公式为赢奖概率(p)乘以每个投注可能赢得的金额,然后减去损失概率和每个投注损失金额的乘积。因为损失概率等于1(或100%)减去赢奖概率,所以该公式可简化为以下公式:
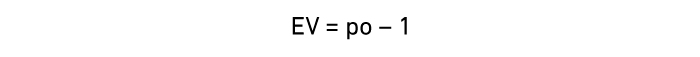
“o”代表博彩公司提供的欧式小数赔率。预期价值对于所有博彩玩家来说都是最重要的数字,因为他们可以从中得知自己能否获得长期的投注利润。
博彩玩家找到预期价值后,他们必须立刻决定要投注多少资金。18世纪数学家丹尼尔·伯努利明白只有蛮干的傻子才会完全根据客观预期价值来决定要冒多少风险,而不考虑投注带来的主观结果,即期望获得(或损失)什么。这种主观上的期望称作效用。
不确定性下的效用
我们面前有两个箱子。第一只箱子里装有€10,000现金。第二个箱子里要么有€20,000现金,要么空无一物;我们不知道打开箱子后会出现哪种情况,但是这两种结果的概率是一样的。现在,你需要挑选其中一只箱子。你会选哪一个?
“凯利公式在技术上确实可以使赢钱的博彩玩家长期最大化他们的资金规模”
这是一个经典的效用谜题。从数学上来说,这两个箱子有相同的预期价值,即€10,000。如果你无限次地重复这个游戏,那么选哪个箱子都是一样的。然而,在这个游戏中,你只能选择一次。大数法则在这里并不适用。
选择第一只箱子,你一定会拿到€10,000。选择第二个箱子,你就会遭遇偶然性:运气好的话,你会拿到€20,000;运气不好的话,空手而归。不出所料,大部分人在面对这么大一笔钱时都选择了一定有钱的第一只箱子。
从效用的角度看,一定能拿到的€10,000绝对比可能什么都没有好得多。面对相同的数学预期值时,那些觉得确定性比冒风险有更大效用的人都存在风险厌恶。
如何计算最佳投注本金?
丹尼尔·伯努利认为,当需要在不确定性条件下做出决策时,人们的标准理性行为是风险厌恶。他由此对自己的假设进行了量化:“财富的任何小幅增长带来的效用都与之前拥有的物资量成反比。” 换言之,你已经拥有的财富越多,更多财富为你带来的效用就越少。这种效用函数是对数的,通常被称为财富的边际效用递减。
“尽管使用凯利公式会导致回报的巨大波动,但是它确实可以使赢钱的博彩玩家长期最大化他们的资金规模”
丹尼尔·伯努利的理论更为实用的应用之一是众多博彩玩家熟知的资金管理方式凯利公式。1956年,约翰·凯利在AT&T贝尔实验室工作时,为了解决长途电话线噪声而提出了该公式。没过多久,赌徒和投资人很快就将该公式用于优化资金管理和利润增长。
虽然凯利的动机完全不同于伯努利,但是他的公式在数学上却等于对数效用函数。实际上,它指导博彩玩家将自己总资金的一定百分比用于投注,这个百分比和预期价值(EV)成正比,和成功的概率成反比。
我们知道EV = po – 1(p是成功的“真实”概率,o是投注的欧式赔率),因此可以如下计算出凯利投注百分比(K):
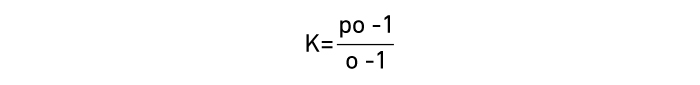
本质上,凯利公式最大化了预期对数效用。在投注中使用凯利公式的结果之一是回报的巨大波动,这种特点可能并不能最好地满足所有人对效用的需求。此外,它的使用确实也需要对结果的“真实”概率进行精确估计。
无论如何,凯利公式在技术上确实可以使赢钱的博彩玩家长期最大化他们的资金规模。当然,要做到这一点,博彩玩家必须找到这样一家博彩公司:他们不会因为特定的资金管理策略(比如凯利公式)而起疑,也不会在玩家持续赢钱时限制他们的投注行为。在这一点上,Pinnacle有着业内无人可望其项背的卓著声誉。



